算法时间复杂度(Big-Oh)
关于Big-Oh
首先Big-Oh($O$)是用来描述一个函数的渐进行为的工具。
关于Big-Oh的正式定义(数学定义):wikipedia
例子:
$n^3+3n^2+2n+1 = O(n^3)$
$0.000000001n^3+3n^2+2n+1)=O(n^3)$
$nlog^n+n=O(nlog^n)$
常见的Big-Oh类型
- 常数(Constant)$O(1)$
- 对数(Logarithmic)$O(log^n)$
- 开方(SquareRoot)$O(\sqrt{n})$
- 线性(Linear)$O(n)$
- 对数线性(Linearithmic loglinear quasiliear)$O(nlog^n)$
- 平方(Quadratic)$O(n^2)$
- 指数(Exponential)$O(k^n)$
Big-Oh in a (set of) image(s)
原图摘自 这里
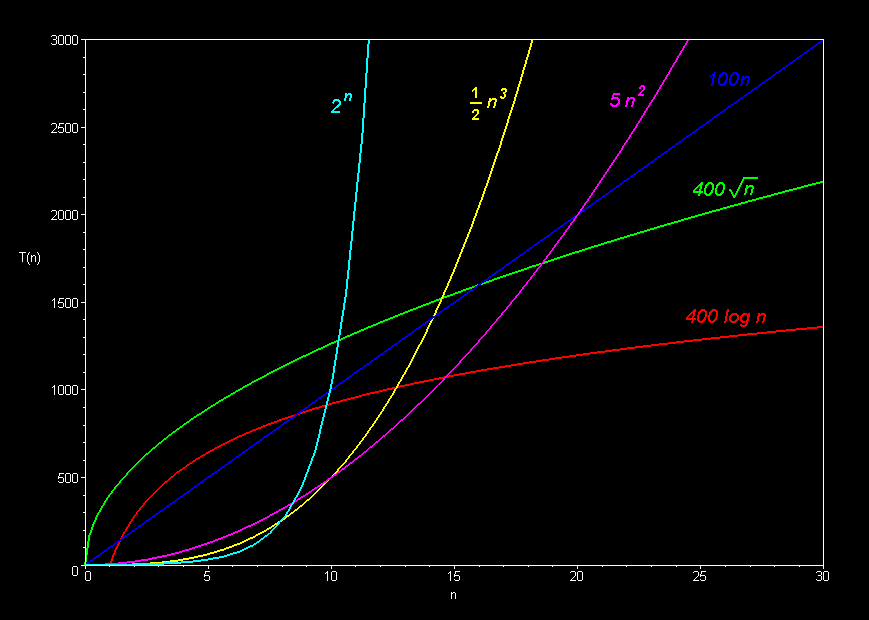
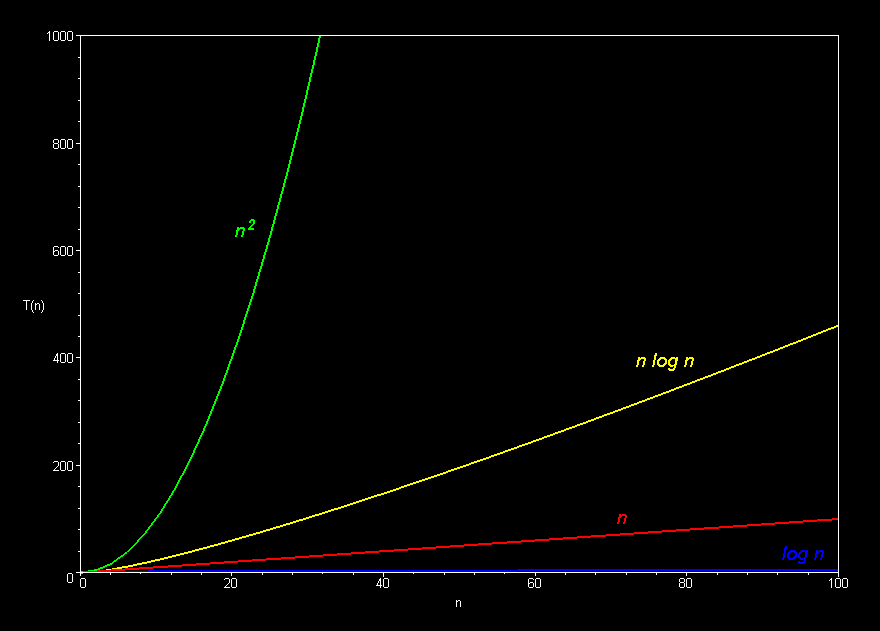
常见操作的Big-Oh
| 操作 | List | Set/Dictionary |
|---|---|---|
| length(len()) | $O(1)$ | $O(1)$ |
| L.append(item) | $O(1)$ | – |
| Add | – | $O(1)$ |
| Copy | $O(N)$ | $O(N)$ |
| max(L) | $O(N)$ | – |
| min(L) | $O(N)$ | – |
| insert | $O(N)$ | $O(1)$ |
| delete | $O(N)$ | – |
| remove | $O(N)$ | $O(1)$ |
| val in L | $O(N)$ | $O(1)$ |
| L.count(val) | $O(N)$ | – |
| L.sort() | $O(Nlog^N)$ | – |
| L.sort(reverse=True) | $O(Nlog^N)$ | – |
| Get/set item | $O(1)$ | $O(1)$ |
| Iteration(for 循环体) | $O(N)$ | $O(N)$ |
更多操作查看:这里
Big-Oh运算法则
加法法则
$$O(f(n))+O(g(n)) = O(f(n)+g(n))$$
例如:
$O(N)+O(log^N) = O(N + log^N) = O(N)$
$O(N)+O(Nlog^N) = O(N+Nlog^N) = O(Nlog^N)$
乘法法则
$$O(f(n)) \cdot O(g(n)) = O(f(n) \cdot g(n))$$
例如:
$O(N) \cdot O(log^N) = O(N \cdot log^N)$
$O(N) \cdot O(N^2) = O(N \cdot N^2) = O(N^3)$
看到这你会说,看起来不错,但有什么用呢?
首先有了加法法则可以帮助我们理解顺序执行的程序段是怎样的复杂度。
举个例子:
如果一段程序调用了两段子程序$f(…)$和$g(…)$,他们在程序段内的调用顺序是:
1 | f(...) |
其中$O(f(…)) = N$, $O(g(…)) = N$ 那么这段程序的时间复杂度会是怎样的?
对,$O(f(…)+g(…)) = O(f(…))+O(g(…)) = O(N+N) = O(N)$
什么太简单了?
来个带分支判断的:程序结构如下
1 | if test: |
令test的复杂度为$O(T)$, block1的复杂度为$O(B1)$ block2的复杂度为$O(B2)$, 那么这段程序的复杂度是怎样的?
其次乘法法则可以帮助我们理解由循环控制的程序段的复杂度。
举个例子:
程序结构如下:
1 | for i in range(N): |
其中$O(f(…)) = N^2$
那么这段程序段的复杂度为: $O(N) \cdot O(f(…)) = O(N) \cdot O(N^2) = O(N \cdot N^2)$
好的有了这两个工具,相信多数的Big-Oh案例分析能轻松搞定。
常见排序、查找算法复杂度
其实这些算法复杂度都可以通过上面的运算法则以及操作的复杂度推算出来的,但是作为一个可以作为快速备查的cheatsheet下面就直接罗列出结论:
先来查找(search):
| 算法 | 时间复杂度 |
|---|---|
| 线性查找(Linear search) | $O(N)$ |
| 二分查找(binary search) | $O(log^N)$ |
注意这里的前提条件是:
线性查找针对的是无序列表,二分查找针对的是有序列表。
再来排序(sorting):
| 算法 | 时间复杂度 |
|---|---|
| 冒泡排序(bubble sort) | $O(N^2)$ |
| 插入排序(insertion sort) | $O(N^2)$ |
| 归并排序(merge sort) | $O(Nlog^N)$ |
| 选择排序(selection sort) | $O(N^2)$ |
| 快速排序(quick sort) | $O(Nlog^N)$ |
| 堆排序(heap sort) | $O(Nlog^N)$ |
